Index
1Linear
Regression 1
1.1Linear
Regression: One Input One Output 1
1.2Multi
Dimensional Linear Regression 3
2Two
inputs, One Output 4
2.1Definitions 5
2.2Algorithm 6
2.3Execution 6
2.3.1Develop
the Error 6
2.3.2Introduce
Accumulator FOMs 7
2.3.3Partial
Derivatives 8
2.3.4Linear
System of Equations 9
3Multidimensional
Linear Regression Extension 10
3.1Validation 11
4Extend
Regression to multiple output 12
5Error
Metric 13
6Example 13
7Comparison
with gradient Descent 14
8Recap 15
9Conclusions 17
1Linear Regression
Linear regression is a tool to compute
the bias and gain of a linear transfer function between an input and
an output set to achieve minimum square error.
1.1Linear Regression: One Input One Output
Regular linear regression allows to
estimate a linear relationship at minimum square error between one
input set and one output set. It's one dimensional.
Regression of one input vs. multiple
output can be achieved by computing linear regression for each
individual output.
Example: input set X, and output set
Y. Estimate Bias and Gain to achieve set Yest with minimum square
error between Y and Yest.
1.2Multi Dimensional Linear Regression
I extend linear regression so that I
have multiple input sets X0, X1, Xj-1 and multiple output sets Y0,
Y1, ... , Yk.
The idea, is that samples from multiple
input sets can be mixed to lower the square error that would be
obtained by computing all linear regressions individually than
intermixing the results with some proportions.
OBJECTIVE: find the optimal value of
the Bias vector and the Gain matrix to achieve minimum square error
between the output estimate matrix Yest and the training output Y.
OPTIMIZATION: Output sets are
independent of each others. You only need to work out a solution from
many input sets X and one output set Y, than extend that solution to
multiple output dimensions.
2Two inputs, One Output
I consider the first case. A system
with two inputs and one output.
Example
A two inputs one output data set can
be plotted as a 3D point cloud. The points in the input sets lay on
the horizontal plane, the output adds a third vertical dimension.
Multidimensional linear regression tries to use the two inputs sets
to approximate the position of the output. It's a three dimensional
line in which there is one offset in height and two gains that
control the estimated line direction.
Two inputs one output is the limit of
human minds. We are unable to visualize more than three spatial
dimensions. In practice, what a neural network does, is it tries to
fit lines in thousand-dimensional or even million-dimensional and in
future billion-dimensional spaces.
OBJETIVE: Multidimensional linear
regression is used in the DeepOrange architecture to fully compute a
layer/slice of the neural network in one step.
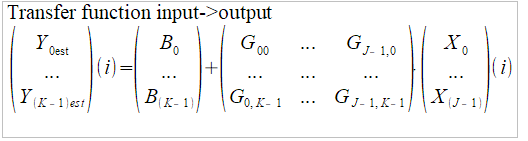
2.1Definitions
Definitions for the math to follow.2.2Algorithm
The algorithm is the same used for deriving the regular linear regression equations- I develop the error to extract dependence on the input and output set only
- I develops the sum series into accumulators that can be computed once at the start of the process and reduce computation of the linear regression in a manipulation of only ??? variables
- I compute the partial derivative of the error in respect of each linear regression parameter
- The minimum of the function is a point of slope zero. I generate one equation per each partial derivative to search for the minimum
- Solving the system for the linear regression parameters gives me the parameters to achieve minimum square error
- By extending the computation to multiple input and output dimension, I can achieve my multidimensional linear regression extracting the closed equations for the bias and both gains in function of the accumulators
2.3Execution
Extract the closed relationship for B,
G0 and G1, the three parameters of the 2->1 Linear regression.
2.3.1Develop the Error
Develop the error. Eliminate dependence
on Yest.
Inject the definition of the estimate
inside the definition of the error metric.
2.3.2Introduce Accumulator FOMs
I use the linearity of the sum to group
all the sum of training vectors into handy accumulators that can be
computed only once with a MAC. Later computations can be done just
using the FOMs, for huge gains in performance and memory footprint.
With this I have the error metric I
want to optimize for in function of the parameters (the thing I want
to find) and the accumulators of the training vectors (my inputs)
2.3.3Partial Derivatives
Objective: find the parameters Bias and
Gain that results in the minimum value of the error metric.
The minimum is a point with a slope of
zero, so the problem translates to finding the combination of Gain
and Bias that results in the derivative of the error being zero.
To make my life easier, I see that the
square root is a monotone function.
If I find the minimum of the argument,
I also find the minimum of the square root.
First I compute the partial derivatives
of the error argument in respect to Bias and Gain.
2.3.4Linear System of Equations
First I tried to brute force the computation like I did with regular linear regression.Now, for the massive intuitive leap: I can represent the system of equations in matrix form.This makes it easy to extend this rule to higher dimensions and allows me to write the system in a compact and understandable way.
3Multidimensional Linear Regression Extension
Seeing the 3x3 case, it's obvious how the solution extends to higher dimensions. I just make the vector longer and the matrix larger. The beauty of matrices is that as long as you write correctly the content, scaling up to higher dataset sizes/dimensions translates the adding rows/columns.3.1Validation
Sanity Check. Test the equations with a
sample sets to make sure the equations are correct. Test case with
two inputs, one output and six samples.
Case 1) A signal guarantees zero error
and the other does not. This make sure the algorithm understands it's
okay to ignore one input set if it brings you away from the correct
solution.
Case 2) Both signals have an error.
Multidimensional Linear regression has to balance the gain of both
sets to achieve an error lower than what individual sets would
achieve.
4Extend Regression to multiple output
Outputs are independent of each others, but I can reuse the same input FOMs.Having defined correctly the form of the matrices the first time around, I again abuse matrix based math. If I want to add output dimensions to my problem, I just add columns/row to the matrices that represent my problem. I extend the content according to the low I identified and voila!
I only need to add the new metrics, and I magically have the full parameter matrix!
It does not gets easier than this.
5Error Metric
Following from regular Linear Regression, the next step would be to obtain the closed form of the error. It's a gargantuan task, I leave it for the next iteration.6Example
Apply the full multidimensional linear regression to an example.7Comparison with gradient Descent
I'm developing multidimensional linear regression specifically for use in neural networks. It's worth looking now at why the approach of gradient descent is so quirky.Gradient Descent tries to invert a layer by computing the partial derivatives. I implemented it, and was jarred by the limitations and instability of this approach that require lots of effort in giving good learning parameters to avoid oscillations and local minimums.
I now understand why:
Gradient descent wildly misses the magnitude and sign of the correction to be made.
In practice, to make gradient descent work great effort is taken in limiting possible values of the sensitivity and take very small learning steps.
Taking small steps, results in very long convergence times.
Now I fully understand WHY gradient descent is so hard to make work in practice.
8Recap
Recap of Multidimensional linear regression equations.9Conclusions
Multidimensional linear regression is a tool that allow estimation of K training output sets from J input training sets. Parameters are computed in order to minimize square error.A neural network layer is just this. A transfer function that apply a linear transformation to a J dimensional input to obtain a K dimensional output.
Given a neural network Layer, I can use multidimensional linear regression to compute in a single step ALL biases and ALL gains/weights to achieve minimum square error on all outputs.














No comments:
Post a Comment